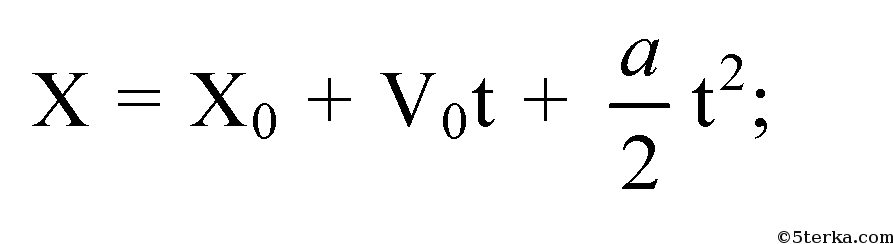
Движение материальной точки является одной из основных концепций физики. Оно представляет собой процесс изменения положения точки в пространстве с течением времени. В данной статье рассматривается движение материальной точки, которое определяется законом x = 0.5t2.
Здесь x обозначает положение точки в пространстве, а t — время. Из данного закона можно понять, что положение точки зависит от квадрата времени. Это значит, что с течением времени точка будет двигаться все быстрее и быстрее, увеличивая свое положение в пространстве.
Движение по данному закону является примером равноускоренного движения, то есть ускорение точки постоянно и равно. Оно можно выразить как a = 1 м/с2. Такое ускорение является положительным и указывает на то, что точка движется в положительном направлении оси x.
Изучение движения материальной точки по закону x = 0.5t2 позволяет лучше понять основные законы физики и применить их на практике. Этот закон находит свое применение в различных областях, включая механику, астрономию, физику тела и другие.
Определение и особенности движения
Одной из особенностей данного движения является то, что скорость точки изменяется с постоянным ускорением: в начале движения ускорение равно 1 м/с2, а с каждой секундой оно увеличивается на единицу. Это означает, что точка будет все быстрее и быстрее двигаться с течением времени.
Другой особенностью является то, что при таком движении точка проходит равные пути за равные промежутки времени. То есть, если за первую секунду точка пройдет 0.5 метра, то за вторую секунду она пройдет уже 2 метра, за третью — 4.5 метра и так далее. Это означает, что путь, пройденный за каждую последующую секунду, будет увеличиваться вдвое по сравнению с предыдущим путем.
Таким образом, движение материальной точки по закону x = 0.5t2 обладает определенными особенностями, которые делают его интересным для изучения и анализа с помощью различных физических методов и понятий.
Определение движения материальной точки
Закон движения материальной точки x = 0.5t² представляет собой квадратичную зависимость, где x — координата точки, t — время. Это означает, что при каждом изменении времени на единицу, координата объекта будет увеличиваться на квадрат половины этого значения времени.
Таким образом, если в начальный момент времени t=0 координата точки равна нулю, то с течением времени она будет увеличиваться согласно закону x = 0.5t². Иначе говоря, точка будет перемещаться все дальше и дальше от начальной точки в соответствии с квадратичной зависимостью от времени.
Определение движения материальной точки позволяет анализировать ее траекторию, скорость, ускорение и другие физические параметры, что является важным для понимания ее поведения и прогнозирования будущих позиций.
Понятие материальной точки в физике
Материальная точка характеризуется своим положением в пространстве, которое описывается координатами. Координаты точки могут быть определены в трехмерном пространстве, например, в системе декартовых координат с осями x, y и z.
Движение материальной точки может быть описано законом, таким как x = 0.5t2, где x — координата точки в зависимости от времени t. Такой закон позволяет определить положение точки в любой момент времени.
Материальная точка также имеет свою массу, которая является мерой инертности точки. Масса определяет влияние точки на другие объекты и влияние других объектов на точку.
В физике материальная точка используется для упрощения сложных систем и является базовым понятием для изучения законов движения и взаимодействия тел. Она позволяет сосредоточить внимание на самом движении, игнорируя детали взаимодействия и внутреннюю структуру объекта.
Важно отметить, что материальная точка является идеализированной моделью, которая упрощает реальные процессы и позволяет получить более простые математические модели для исследования.
Определение движения материальной точки
По данному закону можно определить изменение координаты точки во времени. В данном случае закон движения представляет собой квадратичное уравнение, где координата точки в каждый момент времени вычисляется как половина произведения квадрата времени нашего момента.
Зная закон движения, можно определить множество параметров движения материальной точки, включая скорость, ускорение и траекторию. Например, скорость точки в момент времени t можно найти путем дифференцирования заданного закона движения по времени.
Таким образом, определение движения материальной точки позволяет нам понять, как точка изменяет свое положение в пространстве с течением времени и использовать это знание для решения различных физических задач и прогнозирования будущих положений точки.
Роль закона x = 0.5t^2 в описании движения
Здесь x представляет собой координату точки по оси X в зависимости от времени t. Закон x = 0.5t^2 означает, что координата точки равна половине квадрата времени. Таким образом, закон описывает криволинейное движение, где точка с каждым прошедшим промежутком времени увеличивает свое отклонение от начального положения всё больше и больше.
Этот закон играет важную роль в описании движения и позволяет нам предсказать координату точки при любом заданном моменте времени. Он также помогает определить скорость и ускорение точки в разные моменты времени.
| Время (t) | Координата (x) |
|---|---|
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| 4 | 8 |
Таблица показывает значения координаты точки при разных значениях времени. Очевидно, что с течением времени координата увеличивается пропорционально квадрату времени.
Таким образом, закон x = 0.5t^2 является важным инструментом для описания движения материальной точки и позволяет нам лучше понять зависимость координаты точки от времени.
Закон x = 0.5t^2 и его проявления
Такой закон движения материальной точки имеет ряд интересных проявлений. Во-первых, ускорение движения точки постоянно и пропорционально времени. Это означает, что скорость точки будет увеличиваться равномерно с течением времени.
Во-вторых, формула x = 0.5t^2 говорит о том, что зависимость координаты от времени будет квадратичной. Это означает, что с увеличением времени изменение координаты будет увеличиваться нелинейно, а с ускорением.
Такое движение материальной точки характерно для объектов, падающих с высоты с постоянным ускорением свободного падения. Например, это может быть камень, брошенный вертикально вверх или шарик, падающий с высоты. В обоих случаях координата точки будет меняться в соответствии с законом x = 0.5t^2.
Также, этот закон может быть использован для моделирования движения других физических систем, где присутствуют константное ускорение. Например, он может быть использован для изучения движения автомобиля при торможении на постоянном ускорении или для анализа движения пули, покинувшей ствол пушки.
Важным аспектом этого закона является то, что он описывает лишь одну из возможных формул движения и не учитывает другие факторы, такие как сопротивление воздуха или другие силы, действующие на объект. Поэтому, в реальной жизни движение материальной точки может быть более сложным и требовать более сложных уравнений.
Связь закона x = 0.5t^2 с понятием положения
Закон движения материальной точки x = 0.5t^2 позволяет описать положение точки в пространстве в зависимости от времени. Данный закон указывает на связь между значением времени и соответствующем положением объекта.
Здесь переменная x обозначает положение точки, а t — время. Уравнение закона движения x = 0.5t^2 говорит нам, что положение точки (x) зависит от значения квадрата времени (0.5t^2).
С ростом значения времени (t) значение положения (x) будет увеличиваться квадратично. Это значит, что при увеличении времени точка будет двигаться все быстрее, пропорционально возрастанию квадрата времени. Таким образом, закон x = 0.5t^2 позволяет нам определить положение точки в конкретный момент времени.
Понятие положения играет важную роль в физике и других науках. Оно помогает определить расположение объекта в пространстве относительно определенной точки или системы координат. Понятие положения также связано с понятием перемещения, скорости и ускорения, которые являются дополнительными характеристиками движения.
Таким образом, закон x = 0.5t^2 помогает нам понять, как изменяется положение объекта во времени и как связаны эти две величины.
Понятие положения в физике
Положение объекта может быть задано числовыми значениями, такими как координаты x, y, z в трехмерной системе координат. Например, для движения материальной точки по закону x = 0.5t^2, положение можно определить по числовым значениям времени t и координаты x.
Понятие положения также связано с понятием перемещения. Перемещение — это векторная величина, которая определяет изменение положения объекта. Вектор перемещения указывает направление и длину пути, пройденного объектом, относительно начального положения.
В физике стандартной системой координат является прямоугольная система координат, где оси x, y и z пересекаются под прямым углом друг на друга. Такая система координат позволяет точно определить положение объекта в трехмерном пространстве.
Положение объекта может быть описано как абсолютное, когда оно указано относительно фиксированной точки, или как относительное, когда оно указано относительно другого объекта или системы координат.
Понимание и учет положения объекта являются важными аспектами в физике, поскольку они позволяют анализировать и предсказывать его движение и взаимодействие с другими объектами.
Проекции движения на координатные оси
Движение материальной точки по закону x = 0.5t2 можно разложить на движение по координатной оси x и по координатной оси t. Проекция движения на ось x будет значением координаты x для каждого значения времени t. Проекция движения на ось t будет значением времени t для каждого значения координаты x.
Для удобства анализа проекций движения на координатные оси, можно представить их в виде таблицы:
| Время (t) | Координата (x) |
|---|---|
| 0 | 0 |
| 1 | 0.5 |
| 2 | 2 |
| 3 | 4.5 |
| … | … |
Таким образом, проекции движения точки по закону x = 0.5t2 на координатные оси можно анализировать, используя значения времени t и координаты x, представленные в таблице. Это позволяет лучше понять динамику движения и его закономерности.
Вопрос-ответ:
Какое уравнение описывает движение материальной точки в данной задаче?
Движение материальной точки описывается уравнением x = 0.5t^2.
Какова физическая интерпретация формулы x = 0.5t^2?
Формула x = 0.5t^2 описывает зависимость координаты материальной точки от времени при движении с постоянным ускорением.
Как изменяются координата и скорость материальной точки со временем?
Координата материальной точки изменяется квадратично с течением времени, а скорость линейно возрастает.
Какова физическая интерпретация коэффициента 0.5 в уравнении движения?
Коэффициент 0.5 в уравнении движения олицетворяет половину ускорения материальной точки.
Какие еще уравнения могут описывать движение материальной точки с постоянным ускорением?
Другие уравнения, описывающие движение материальной точки с постоянным ускорением, могут быть вида x = vt + 0.5at^2 или v^2 = u^2 + 2ax, где v — скорость, t — время, a — ускорение, x — координата, а u — начальная скорость.
Какое уравнение описывает движение материальной точки по закону x = 0.5t2?
Уравнение x = 0.5t2 описывает движение материальной точки по закону равномерного прямолинейного движения, где координата точки (x) зависит квадратично от времени (t).